
Quadratics
Standard Form
The standard form of an equation is another representation for a quadratic relation. The standard form of an equation can be shown as:
y = ax^2 + bx + c
In this equation, a, b and c are the known value.
'x' is the variable, which means that it is an unknown value.
As it was possible with all the other forms of a quadratic equation, the zeros, axis of symmetry and the optimal value can be found using the standard form.
Zeros
To find the zeros of a parabola using standard form, it is very simple, since there is formula that could be used to find the solutions. This formula is called the Quadratic Formula. The Quadratic Formula is:
Now plug in the values a, b and c into this formula to find the solutions.
However, it may be apparent to you that there is a plus/minus sign in the equation. This refers back to squares and square roots.
But, all that this plus or minus really means is that there are two possible solutions:
This makes sense because in a parabola there are 2 zeros:
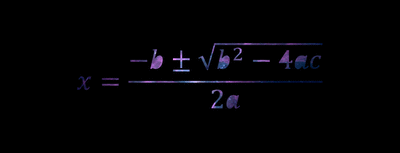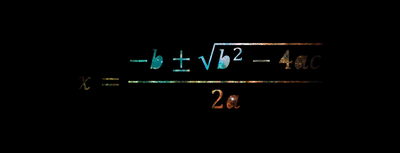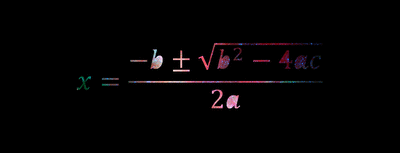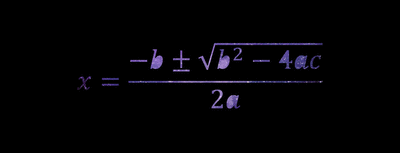

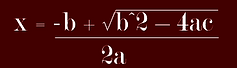

There are some exceptions to a parabola having 2 zeros sometimes, as sometimes, parabolas can only have one or even none zeros.
To figure out how many solutions a parabola has, the discriminant could be used.
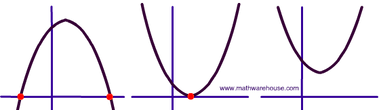
2 solutions 1 solution No solutions
Discriminant
The discriminant is the expression (b^2 - 4ac) which is found under the radical sign in the quadratic formula. To determine the number of solutions that a quadratic relation has, the a,b, and c values of the quadratic relation could be subbed into the discriminent expression to find the total number of solutions. This works like this:
-
If the discriminant is negative, then there will be no solutions.
-
If the discriminant is possitive, there will be 2 solutions.
-
If the discriminant is equal to 0, there will be no solutions.
0 = 6x^2 + 12x + 6
EXAMPLE
0 = 2x^2 + 9x - 7
9 = 4x^2 + 2x - 7
b = 12
a= 6
c = 6
D = b^2 - 4ac
D = (12)^2 - 4(6)(6)
D = 144 - 4(36)
D = 144 - 144
D = 0
Since the discriminant is 0, there are no solutions.
b = 9
a= 2
c = -7
D = b^2 - 4ac
D = (9)^2 - 4(2)(-7)
D = 81 - 4(-14)
D = 81 - 16
D = 65
Since the discriminant is 65>0, there are 2 solutions.
b = 2
a= 4
c = -7
D = b^2 - 4ac
D = (12)^2 - 4(6)(6)
D = 144 - 4(36)
D = 144 - 144
D = 0
Since the discriminant is 0, there are no solutions.
0 = 4x^2 + 2x - 7 -9
0 = 4x^2 + 2x - 16
Since this equation is not equal to 0, so you must move the 9 over to make it equal to 0.
How to solve using the quadratic formula?
To solve using the quadratic formula, just sub in all the values of the quadratic relation into the formula and then solve!
5x^2 + 12x + 7
EXAMPLE

-
-
-
-
-