
Quadratics
Transforming Parabolas
Vertex Form
The vertex form of a quadratic relation is represented by the equation y = a(x-h)^2 + k. To understand transformations, it is essential to know the three main transformations of parabolas:
y = a(x-h)^2 + k
The 'a' value in vertex form causes the graph to be thin or wide. In other words, it causes the graph to have a vertical stretch or a vertical compression.
The 'h' value in vertex form makes the parabola move to the left or right. This movement of the parabola is known as the horizontal translation.
The 'k' value in vertex form makes the parabola move up or down. This movement of the parabola is known as the vertical translation.
In order to transform a parabola, it is useful to first write all the values of the equation which will affect the position of the parabola on the graph.
Next, you should work with the a-value first as it will cause the parabola to stretch or compress. In order to find the coordinates of a parabola after a vertical stretch or compression, first write find the values of the parent function of a parabola and simply multiply the y-values by the a-value of the equation. Also, if the a-value is greater than 0, there will be a vertical stretch, which will cause the parabola to look thin and if the a-value is less than 0, there will be a vertical compression, which will cause the parabola to look wider. Note that the a-value will affect the y-values of the parabola.
Now that you have the coordinates of the parabola after being affected by the a-value, there are three simple steps to follow:
1.
First look for a negative in front of the a-value in the equation. If the a-value is negative, the parabola will be reflected in the x-axis. This means that all the new x-values of the parabola (the x-values after a vertical stretch/compression) will now be negative.
2.
Now, identify the 'h' value in the equation, as it will make the parabola move left or right. It is important to note that if the h-value is negative, then the parabola will move to the right, but if it is positive, the parabola will move to the left.
3.
The final translation is a vertical translation, or in other words moving the parabola up or down. In order to do so, simply identify the k-value in the equation, then look out for a negative in front of the k-value, since if the k-value is positive, the parabola will move up and if it is negative, the parabola will move down.
This is all you need to transform a parabola!
Steps of Transforming Paraboals
Example: y= -2(x+9)^2 + 19
a = -2
h = -9
k= 19
a = -2
h = -9
k= 19

In this example, there is a vertical stretch as the a-value is 2, which is greater than 0.

In the graph above, the red parabola is the parent function. The blue parabola is retrieved after working with the a-values of the equation. Since the blue parabola seems to be thinner, and the parabola changed by a factor of 2, it is a vertical stretch. The last parabola is green and it is simply a reflection of the blue parabola at the x-axis as the a-value of the equation is negative.

Since the h-value is positive 9 in the brackets, it will cause the parabalo to move 9 places to the left.
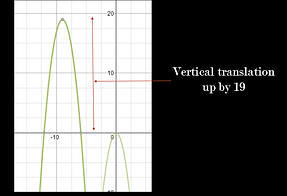

The final parabola should look like this! Also, note that the vertex of the parabola is (-9,19), which is the same as the vertex that would be identified using the vertex form equation, as the vertex is (h,k).