Quadratics
Vertex Form Terminology
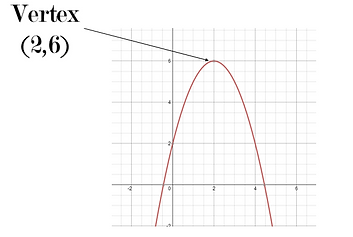
Vertex
The vertex of a parabola is the maximum or minimum point on the graph where the graph changes direction.
This point on the graph is also where the parabola meets the axis of symmetry and the optimal value.
In the vertex form of a parabola, the vertex is expressed as the coordinate (h,k), since the axis of symmetry of a parabola is also the h-value of the vertex form, while the optimal value is the k-value in vertex form.
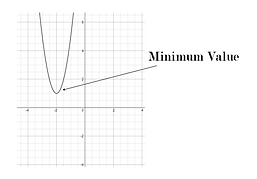
Maximum or Minimum Value
The maximum value is the highest point on a parabola, while the minimum value is the lowest point on the parabola. If the parabola has a maximum value, it will open downwards and if the parabola has a minimum value, it will open upwards.

Optimal Value
The optimal value of a parabola is the y-coordinate of the vertex. This is the y-value where the parabola meets the axis of symmetry.
Since the optimal value is the y-value of the vertex, it is also the k-value in the vertex form of the parabola. Therefore, the optimal value of a parabola can be expressed as y=k.

Axis of Symmetry
The axis of symmetry is the line passing through the vertex of a parabola, which divides the parabola into halves.
The axis of symmetry is the x-value of the vertex, which means that it is also the h-value of the vertex form of a parabola. Therefore, the axis of symmetry can be expressed as x=h.

Zeros
The zeros of a parabola are also known as the x-intercepts or the roots. These zeros are when the parabola crosses the x-axis of the graph. There can be a possibility of two zeros, one zero or no zeros of a parabola.