
Quadratics
Step Pattern
Step pattern is another method of transforming parabolas. Let's see how this works:
First we need to look at the parent function of a quadratic relation.
y = x^2
Now, we will graph this equation. To graph, first make a table of values to find the coordinates of the parabola.
y = x^2
-3 9
-2 4
-1 1
0 0
1 1
2 4
3 9
x x^2
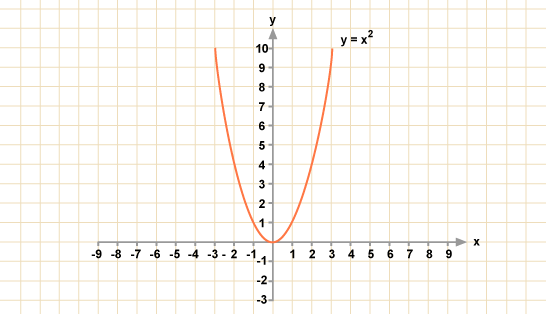
This is an image of the parent function graphed.
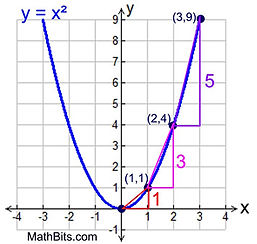
In order to calculate the step pattern of a quadratic equation, start at the vertex, go over one at the x-axis and count the number of times that you need to go up the y-axis until you meet the second point on the graph. Do the same for the rest of the points and the pattern that you should get, would be 1, 3 and 5 as shown on the graph to the right.
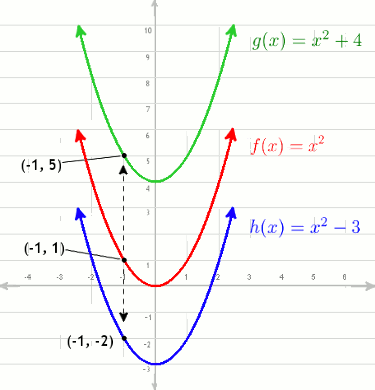
Now, we need to apply the step pattern to other equations. When graphing using the step pattern, multiply the a-value in the equation by the step pattern, to get the new step pattern. This means that instead of going over one and up one, you will go over one and up according to your new step pattern.
To finish the transformations, move the parabola to the left or right and up or down according to the h- and k-values in the equation. After the vertical stretch/compression, horizontal and vertical translations are done, you will have your new parabola!
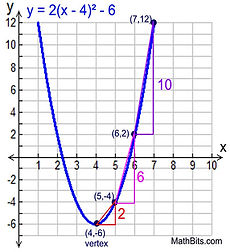
In this example, instead of going over one and up 1, we went over 1 and up 2, since the new step pattern in 2, 6, 10... We got this new step pattern by multiplying the a-value, which was 2 by the original step pattern (1,3,5).