
Quadratics
Standard Form
Axis of Symmetry
When finding the axis of symmetry using standard form, there are 2 ways to get the answer.
The first method is to add the zeros and then divide the answer by 2. However, in order to find the axis of symmetry using this method, you need to find the zeros first using the quadratic formula.
The second method is to use the axis of symmetry equation, which is x = -b/2a. Now, you just need to sub in all the values into the expression and then solve to find the axis of symmetry!
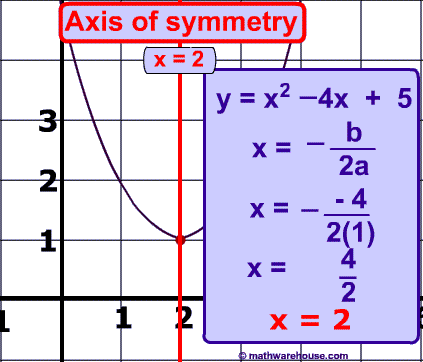

EXAMPLE
y = 5x^2 + 12x + 7
Axis of Symmetry = -1 + (-1.4)
2
= -1.2
Therefore, the axis of symmetry is 2.
Optimal Value
When finding the optimal value, all you need to do is sub in the axis of symmetry into the standard form equation, and then solve. However, before finding the optimal value, it is important to find the axis of symmetry, either using the zeros or the equation for axis of symmetry.
EXAMPLE
Using the axis of symmetry found in the previous example, sub it into the quadratic equation to find the optimal value.
Axis of Symmetry = -1.2
y = 5(-1.2)^2 + 12(-1.2) + 7
y = 5(1.44) - 14.4 + 7
y = 7.2 -14.4 + 7
y = -0.2
Therefore, the optimal value of the equation y = 5x^2 + 12x + 7 is -0.2.
y = 5x^2 + 12x + 7
Therefore, the axis of symmetry is -1.2.